Cracking the Coding Interview: Q 2.6 Circular Linked List Problem

Recently I’m working on “Cracking the Coding Interview 5th Edition”. All my solutions are public on Github. For this typical question about circular linked list in chapter 2, the way to solve it is a bit tricky.

Question

Given a circular linked list, implement an algorithm which returns node at the beginning of the loop.

DEFINITION

Circular linked list: A (corrupt) linked list in which a node’s next pointer points to an earlier node, so as to make a loop in the linked list.

EXAMPLE

Input: A -> B -> C -> D -> E -> C [the same C as earlier]

Output: C

Solution 1

As every node in linked list has an unique address, we can use hash map to record nodes we have visited. By traversing the whole list, the loop beginning node will appear twice sooner or later. In C++, using container set is qualified here.

The implementation is post below.

#include <iostream>;
#include <set>;

using namespace std;

typedef int elemtype;
typedef struct list{
    elemtype data;
    struct list *next;
}*node;

node FindCircle(node head);

int main(int argc, const char *argv[])
{
    /* Make gcc happy */
    return 0;
}

/* implemented with approximate hash table */
node FindCircle(node head) {
    set<node>; buffer;
    node start;

    for (start = head; start != NULL; start = start->;next) {
        if (buffer.find(start) != buffer.end()) {
            return start;
        }
        else {
            buffer.insert(start);
        }
    }

    return NULL;
}

Solution 2

This method is exactly the same with solution on the book. But here I’ll prove it with my own understanding.

The general idea is that using two pointers to traverse the list, one fast, one slow. The speed of slow pointer is 1 and faster pointer is 2. If the linked list has a loop in it, two pointer will meet somewhere in circle. So the question becomes how to find the beginning of loop after two pointer meet.

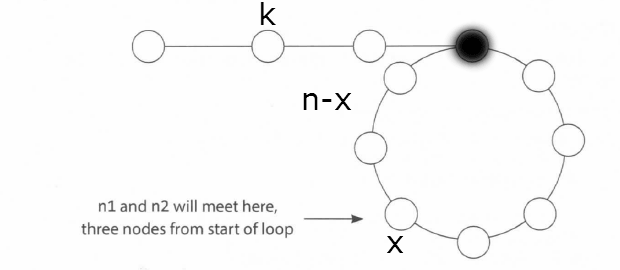Assume the list has a “non-looped” part of length k, the length of loop circle is n. Two pointers meet at length of x over the loop beginning pointer. In other words, they are n-x length behind the loop beginning pointer.

When two pointer meet, fast pointer has moved 2m steps and slow pointer moved m steps repectively. It’s easy to prove,

m = k + x
2m = k + pn + x

Thus,

2m - m = pn, p = 1, 2, 3, 4…

So,

m = k + x = pn

k = pn - x
  = (p - 1)n + (n - x)

From last equation, it’s clear to see that if we put fast pointer back to list head and let it move with speed 1. As both pointers continue to move forward, they will meet again at the loop beginning position.

The implementation can be found on book.